Of running multiple regexp at once

New job, new life

I changed job ! I recently joined Dataiku. We’re creating the perfect Data Science Platform. And so far, it has been pretty awesome… By the way we are still recruiting, so if you are looking for a job in a top notch tech startup in Paris, drop me an email : paul.masurel at dataiku.com.

Back to today’s subject. Last week I was discussing with a colleague at work about the painful lack in Java for an equivalent of re2.

re2 is regular expression matching library open sourced by Google and it is blazing fast. It also makes it possible to compile several regular expression together, which we might have a use for at Dataiku. Basically matching N patterns against a string of length L has a complexity linear in L with re2. Yes you read that well. It is theoretically independant from the number of the patterns.

(A friend pointed me out a library)[https://twitter.com/sylvainutard/status/390378369168461824] to manipulate finite state deterministic automaton in Java : dk.brics.automaton. So guess what I did last week-end? I implemented the part that compiles several patterns together. You can get it and use it (MIT License) on github.

Using it is as simple as :

MultiPattern.compile(
        "ab+",     // 0
        "abc+",    // 1
        "ab?c",    // 2
        "v",       // 3
        "v.*",     // 4
        "(def)+"   // 5
);
int[] matching = multiPattern.match("abc"); // return {1, 2}

But how does it work?

Regular expressions …

(source: XKCD )

Regular expressions are by far the most successful DSL ever. While most programmers have mastered their use, it can become pretty useful to understand how they work. First, a good low-level understanding helps when dealing with regexp related performance bottleneck, and second, what you’ll find under the hood is awesome.

Let alone Perl regular expressions for the moment, a regular expressions are defining what is called a formal language . Basically they are boolean function which says whether a string matches or not.Not all of such function can be expressed as regular expressions. For instance, string that have as many a than b cannot be written as regular expressions.

Actually a formal language that can be described with regular expression is called tautologically a regular language in Chomsky hierarchy.

But let’s stay practical. What happens when I try to match a string with .*ab ?

.. are all about automata

The regular expression is parsed and compiled into the following automaton.

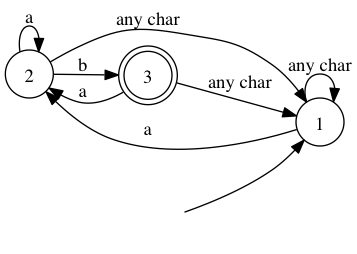
How do we read this thing? A finite automaton has a finite number of states, those are the three circles. State 1 is our starting state. In the beginning it is the only active state. When trying to match a string against a regular expression, we just scan through the character of the string, and update the list of activated states by going through all of the active states and follow the arrow matching the character.

Once the whole string has been scanned, deciding whether the string is matching or not is just a matter of looking at the ending states.

Here only state 3 is marked as valid. If one of the matching state is valid, the regular expression is matching.

For instance, when matching the string aab, the automaton will start with {1} and will go have successively the following states activated : {1,2}, {1,2} and finally {1,3}. 3 is matching and therefore the string is matching. Notice how more than more than one state was activated at the same time. This is why such an automaton is called nondeterministic.

On the other hand, deterministic automaton can have only one state activated at a time. These latter perform better because only one arrow is followed per character. Their performance is straightforwardly linear with the number of character.

With non-deterministic automaton, things can be hairy.

Powerset transformation to the rescue

For this very reason, it is very often a good idea to convert our finite nondeterministic automaton into a deterministic one. This is done by using the so-called powerset transformation. The idea is to consider the power set of the state of our automaton. If you are not familiar with the concept, it is the set of the subset of the state of our automaton. Our nondeterministic automaton having only three states, it is actually possible to enumerate all of the elements of its powerset: ∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}. If we have N states in the beginning, its powerset has 2^N elements.

After consuming k characters, let’s consider the subset of activated states. Given the next character of the string we will reach another subset of activated states. We can therefore built up a deterministic automaton by using nodes labelled with subsets of the non deterministic automton.

In our case, the automaton will look as follows.

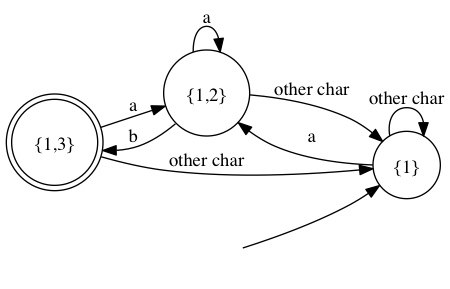
Luckily enough our automaton have only 3 states… Yet deterministic automaton are typically bigger than their non-deterministic counterpart. Hence, you can put this trick in the memory vs cpu trade-off box.

Matching more than one regular expression

Matching the same string against many regular expression is a very common problem. Imagine a weblog on which you want to extract statistics. You might want to identify different part of your website using regular expression applied on the urls. If you are in e-commerce, we are probably talking about hundreds of regular expression. Your for-loop on the regular expressions might be a little too CPU intensive.

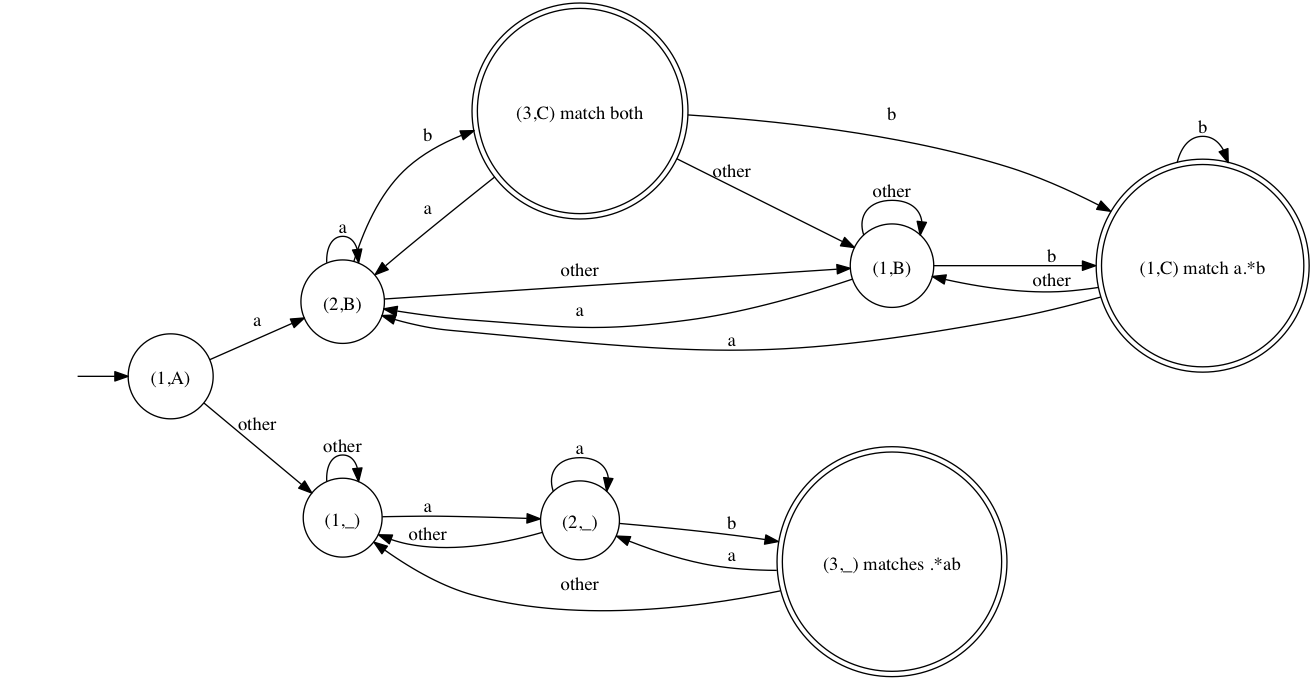
We can use a trick very similar to that of the powerset transformation. Instead of consider a powerset, we just consider labelling the states with the cartesian product of the set of states of all of the regular expression respective automata.

Matching state will then hold the set of matched regular expressions.For instance we can try and merge the previous automaton with the automaton matching a.*b.

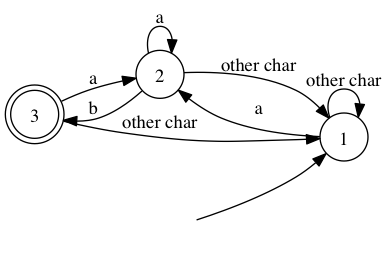
Once relabelled, automaton for .*ab looks like this

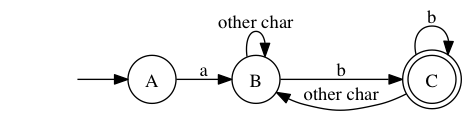
a.*b’s deterministic automaton looks like this.

And the deterministic automaton matching both a.*b and .*ab looks as follows.

Thanks to evmar for correcting me : V8 does not use re2.