Of caret awareness
Caret Awareness : A neat feature for autocomplete
Around 8 years ago, I read the description of a nice UI improvement to the traditional autocomplete search box. I cannot recall the name the author used for the feature, but I like to call it caret awareness. (caret is just another fancy name for text cursor).
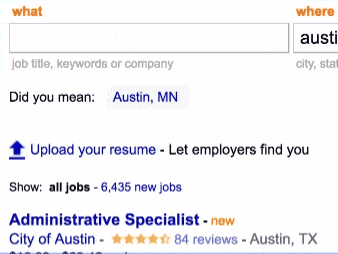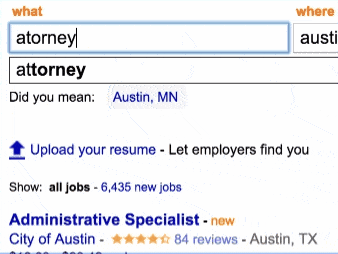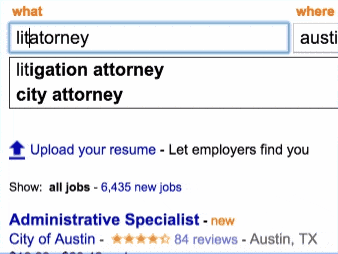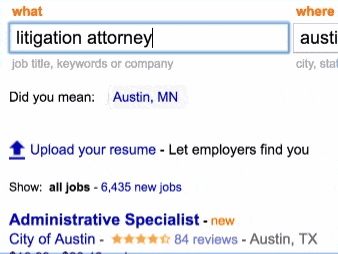
Here is the problem it was addressing. When I search for something, and the results do not seem accurate, I like to add an extra keyword to refine my query. Sometimes (especially in English), it makes more sense to prepend than to append this keyword. In that case I bring the caret at the beginning of the search box and start typing my extra keyword.
As I am typing these new words, an autocomplete system strictly working on prefix matching will have a hard time offering me any suggestion.
“BarObama”, what the hell is this user searching for?
The idea of caret awareness is to send the autocomplete service the position of the caret along with the query. For the query above, the request to the service is along the line of
?q=BarObama&caret=3
So we added the feature to indeed.com. Here is how it looks like.
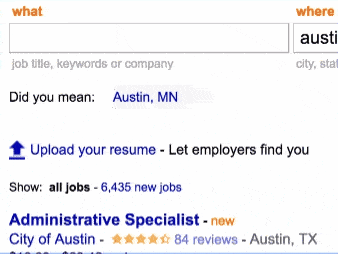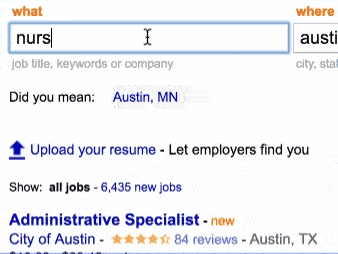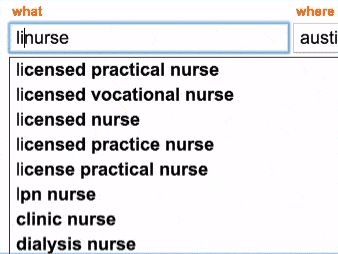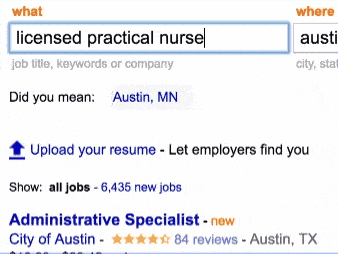
This feature can be implemented in different ways. But here comes the twist : our autocomplete is also fuzzy : if your query is long enough, it will start considering options that at Levenshtein-Damerau distance of up to 2.
In the following example, even if the user mispelled “attorney”, indeed guessed that “litigation attorney” is really what he trying to type.
Let’s see how it works.
Caret aware Levenshtein automaton for the win!
When I first heard about the existence of Levenshtein automaton, I was very surprised.
A mindboggling implication for instance, is that for any given string $s$ for any given $k$, there is a regular expression that match exactly the strings that are at a levenshtein distance from $s$ smaller than $k$.
While the result is not really practical at all, it is pretty cool isn’t it?
Well actually let’s go further : let’s consider a regular expression $s$.
For instance, ab*c.
It matches an infinite set of strings :
- abc
- abbc
- abbbc
- abbbbc
- …
Let’s now extend this set by adding all of the strings that are at a levenshtein distance of less than 1 from one of the original elements.
We end up with a much larger set. For instance the string below have been added.
- yabc
- ac
- bac
- …
One can show that there once again exists a finite definite automaton (and hence, a regular expression) that matches exactly the strings of this new set.
What does this have to do with caret awareness ?
Well, our caret-aware fuzzy search really is all about trying to find entries in a dictionary
that are at levenshtein distance of 2 of a string that matches the regular expression lit.*atorney.
We now know that there is a DFA, possibly huge, that actually does the job. But can we build it efficiently ?
Building the automaton
*This section is very technical, and assumes you have read my previous blog post about Levenshtein Automata. *
Adapting the implicit NFA approach is relatively simple.
Essentially, we change our transition function
def transitions(self, state, c):
(offset, D) = state
if D > 0:
yield (offset, D - 1)
yield (offset + 1, D - 1)
for d in range(min(D + 1, len(self.query) - offset)):
if c == self.query[offset + d]:
yield offset + d + 1, D - d
by adding the caret information
def transitions(self, state, c, offset):
(offset, D) = state
# we matched up to the caret,
# any character we get can be matched thanks to the ".*"
# pattern, so staying in the same state is always an option
if offset == self.caret:
yield (offset, D)
if D > 0:
yield (offset, D - 1)
yield (offset + 1, D - 1)
for d in range(min(D + 1, len(self.query) - offset)):
if c == self.query[offset + d]:
yield offset + d + 1, D - d
In my previous post, I argued that the implicit NFA solution was not as efficient as the parametric DFA approach of the original paper of Klaus Schulz and Stoyan Mihov. Caret-awereness is very pathological, as the number of states can rapidly explode.
Without caret-awareness, the number of state that can coexist at the same time
was bounded by 2k + 1 where k is the Levenshtein distance considered. For Levenshtein-Damerau, a generous bound would be 2(2k + 1).
With caret-awareness, there is no such bound : the number of states in the NFA grows linearly with the length of the query. More accurately, it grows linearly with the length from the caret position to the end of the string. ouch.
For the same reason, Klaus Schulz and Stoyan Mihov parametric DFA caching trick cannot be applied directly : the parametric DFA would have an infinity of states.
Without going into too much details, what we did is that we approximate the automaton by one that is kind enough to be bounded. The approximation works as follows : when implementing the NFA that is then used to build the parametric DFA, we always trim the set of states by removing the states that have too low an offset. More accurately, if the largest offset is $m$, we remove all states associated with an offset lower than $m - (2k + 1) - 2$.
This approximation only can only create false negatives for terms in the dictionary that includes some long repetitions. For instance if we are searching for I love.*Jar Jar Binks and our dictionary contains I love Jar Jar Binks,
the trimmed automaton will make a mistake because of the repetition Jar coming right after the caret.
So we pre-built a parametric caret-aware automaton for Levenshtein Damerau with a distance of 1, and 2. The resulting file takes around 2MB, and it is shipped with our code.
Once we have that, we can either use a parametric DFA, or build an explicit DFA for our language. We currently built the DFA because it was pretty fast in practise anyway.
The bizarro dictionary
Another issue with caret awareness is that if the caret is toward the beginning of the string, our automaton has to visit all or most of our trie. This phenomenon has nothing to do with fuzziness, so let’s forget Levenshtein for this section.
In the case of l.*atorney, the intersection with the trie will end up exploring
all of words starting by an l.
We solved this problem by processing these queries in what I like to call the bizarro world, where all string are reversed.
In this world, our query: l.*atorney, becomes yenrota.*l, and we will only visit
the string that starts up by yenrota.
This means we ship a bizarro trie along with our original dictionary trie. If the caret is in the second half of the query, we do our regular matching, but if the caret is the first half of the query, then we reverse the query, and run it against our bizarro dictionary.